Sketch
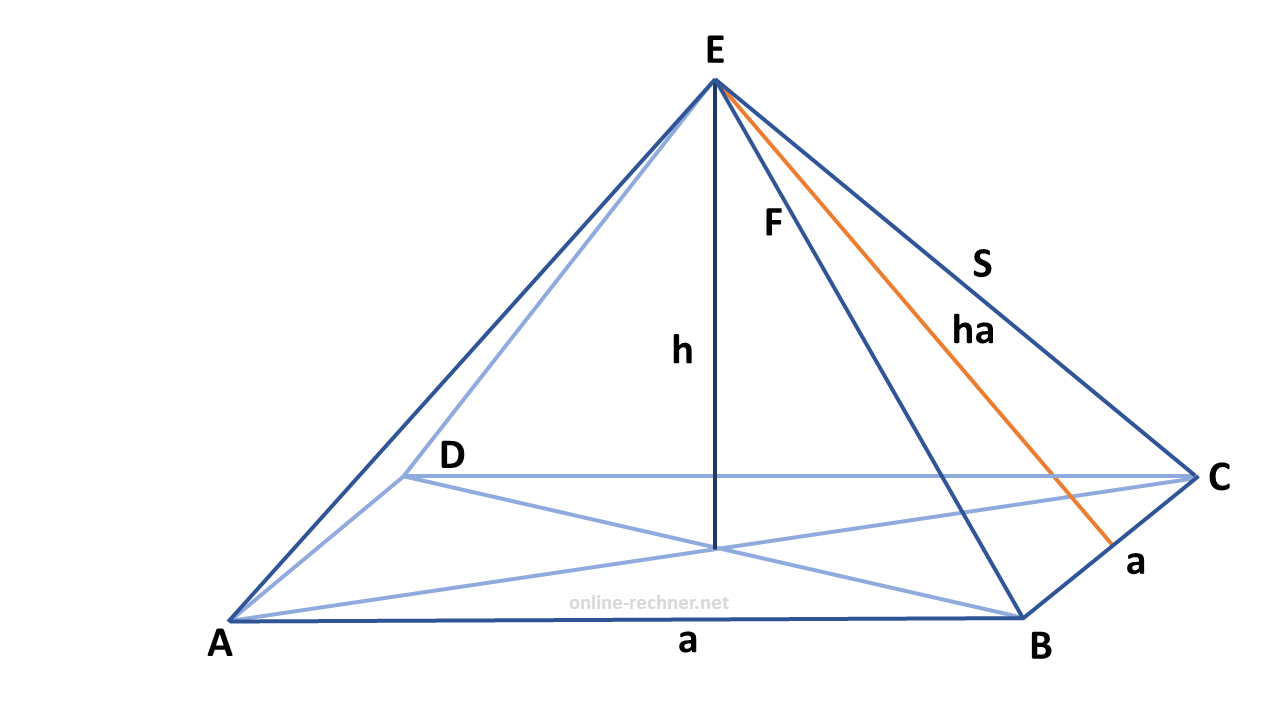
Surface area of a pyramid
Formula: a2 (4 * (1/2 * a * ha)) = O
Base area = a2
Example calculation: 5cm2 (4 * (1/2 * 5cm * 12cm)) = 145cm2
Shell of a pyramid
Formula: 4 * (1/2 * a * ha) = M
Example calculation: 4 * (1/2 * 5cm * 12cm) = 120cm2
Volume of a pyramid
Formula: (G * h) / 3 = V
G = base area of the pyramid (a2)
Example calculation: (5cm2 * 10cm) / 3 = 83.33cm3
The calculation of a pyramid can relate to various aspects, including volume, surface area and edge lengths. Here are some basic calculations that are typically done with pyramids:
1. volume: the volume of a pyramid is calculated by multiplying the base area (A) by the height (h) of the pyramid and dividing the result by 3. The formula is V = 1/3 * A * h. The base area depends on the shape of the base - for example, if it is a square, the base area is simply the side length squared.
2. surface area: The surface area of a pyramid consists of the area of the base plus the area of all triangular sides. For a square pyramid (with a square base and four isosceles triangular sides), the area of each triangular side is calculated by multiplying the base side (equal to the side length of the base) by the so-called "slant height" and dividing by 2. The total area is then the area of the base plus four times the area of one side of the triangle.
3. edge lengths: The length of the edges of a pyramid depends on the specific shape and size of the pyramid. For example, in a square pyramid, all four edges of the base are the same length, while the four edges leading to the top of the pyramid are also the same length, but usually have a different length than the edges of the base.
These calculations require a basic understanding of geometry and trigonometry, especially if the pyramid has more complex shapes, such as a triangular or pentagonal base.
